Machine Learning 笔记（三） 多变量线性回归

注：本文内容资源来自 Andrew Ng 在 Coursera上的 Machine Learning 课程，在此向 Andrew Ng 致敬。

一、多特征（Multiple Features）

笔记（二）中所讨论的房价问题，只考虑了房屋尺寸（Size）一个特征，如图所示：

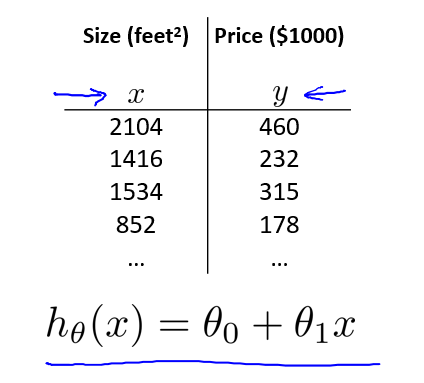
这样只有单一特征的数据，往往难以帮助我们准确的预测房价走势。因此，考虑采集多个特征的数据值，往往能提升预测效果。例如，选取如下 4 个特征作为输入值时的情况：

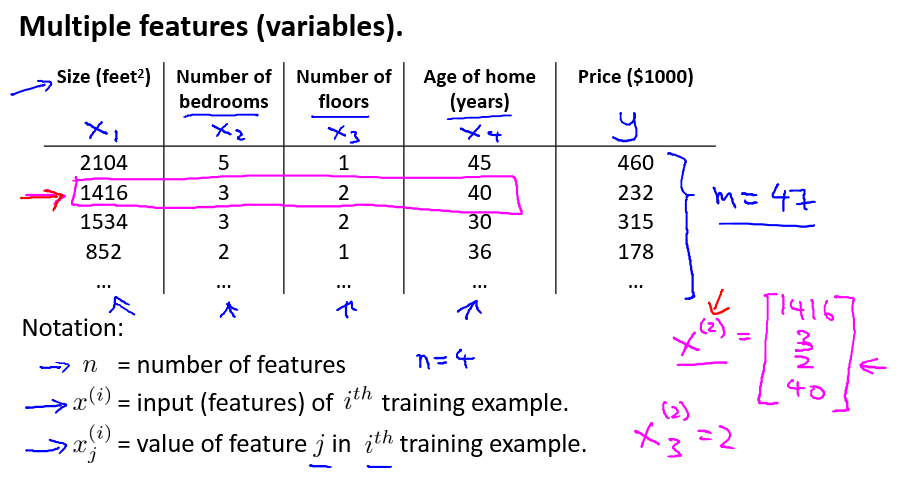
对一些概念的解释：

• $n$: 特征数量
• $x^{(i)}$: 第 $i$ 个训练样本的输入（所有特征）
• $y$: 输出变量/目标变量
• $x_j{(i)}$: 第 $i$ 个训练样本的第 $j$ 个特征的值

对于多个特征，我们需要更新假设函数，以包含所有的输入特征，对于 4 个特征的假设函数如下：

推而广之，$n$ 个特征的假设函数如下图所示。为了方便，我们定义 $x_1=1$ ，采用列向量来表示参数 $θ$ 和 输入 $X$。

这样，假设函数 $hθ(x)$ 可表示为：

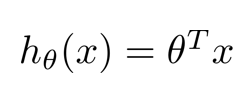
多特征的线性回归问题，被称为 多变量线性回归问题。

二、多变量梯度下降（Gradient Descent for Multiple Variables）

多变量的线性回归问题与单变量类似，由于特征数量从 1 变为 n，所以需要更多的计算。其对比如下：

三、特征规范化（Feature Scaling）

由于现在有多个特征，且各个特征的取值范围有所不同。例如，房屋的尺寸一般在数千左右，然而卧室的个数往往是个位数的，要将他们原封不动地表示在图像中，将会造成大部分的数据都拥挤在一个范围内。极度的不均匀将导致梯度下降速度的减缓，无法进行有效区分。那么，就需要利用特征规范化的方法，将所有特征都限定在一个范围左右。

在上图左就可以看出，由于未进行特征规范化，等值线呈现出扁平化，导致收敛速度较慢。而图右，将房屋尺寸除以 2000，卧室个数除以 5，这样，将两个特征都转化到了 0~1 的范围内，等值线呈现较为均匀的状态，加快了收敛速度

特征规范化

将每一个特征值都转化到同一个特定的范围内（通常选 -1 <= x <= 1）

在特征规范化中，另一个常用的方法是均值标准化（mean normalization）。均值标准化的转化方法如下：

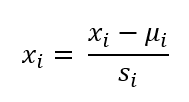
概念：

• μi: 特征 $x_i$ 的均值
• si: 特征 $x_i$ 的范围（最大值-最小值）

例如：在本例中，$x_1$ 和 $x_2$ 的转化如下：

均值标准化

利用特征均值与范围，将特征规范到 -0.5~0.5 的范围内。

四、学习率（Learning Rate）

本节见介绍，如何确认梯度下降正常工作，以及如何选择学习率 α 。

首先，如何确认梯度下降正常工作。我们的目标是最小化 J(θ) ，并希望其在每一轮迭代中都减小，直至最后收敛：

简单的收敛测试方法是：如果 J(θ) 的减小小于一个 ε 值（例如 10-3）是，说明已经收敛。

对于如何选择 α 的问题，在之前的章节已有讲解。如果 α 太小，收敛速度将会很慢，如果 α 太大，J(θ) 可能不会减小，甚至可能最后不收敛。一般情况下 α 通常选择 0.001、0.01、0.1、1 等较小值。

五、特征以及多项式回归（Features and Polynomial Regression）

现在我们了解了多变量线性回归问题。在本节中，我们将讨论特征的选择以及如何用这些特征获得好的学习算法，以及一部分多项式回归问题，它可以使用线性回归的方法来拟合非常复杂的函数，甚至非线性函数。

以预测房价为例。假设你有两个特征，房屋的临街宽度（frontage），以及纵向深度（depth），因而，假设函数如下所示：

当然，我们也可以用其他的方法来表示这个特征，例如此问题中，我们可以创造一个面积特征，它等于宽度与深度的乘积，那么假设函数就可以简化为上图下面所示。

再仔细分析房价问题的训练样本，我们可以粗略地发现，用一条曲线比一条直线效果更好。因此引入多项式回归的概念，以一个多项式假设函数来代替原有的线性函数：

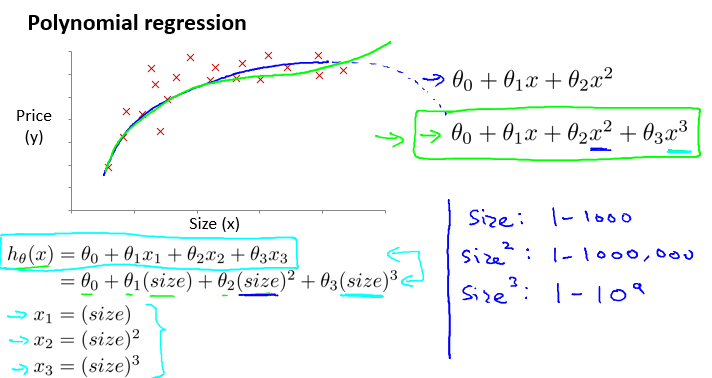
可以看到，如果选择一个二次多项式，可以较好的匹配样本数据，但是当房屋尺寸持续增长时，价格将会呈下降趋势，这与现实是明显不符合的。因而，选择三次多项式可能是一个较好的选择。而且，在此问题中，我们只用了一个特征，即房屋尺寸，却得出了更加复杂的曲线，以带来更加好的效果。

当然，多项式的选择可以是很多种的。我们还可以使用根号函数来作为假设函数，这更加地符合实际情况：

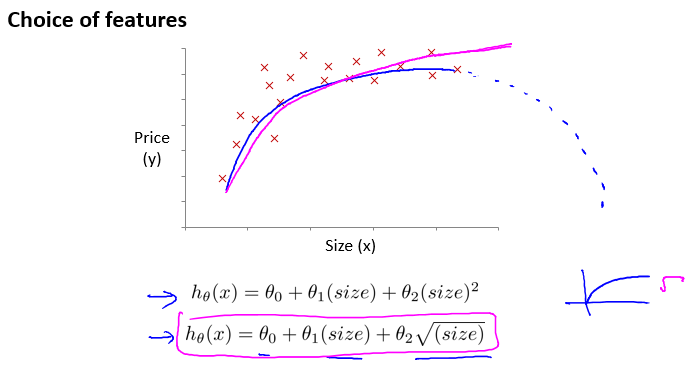
六、正规方程（Normal Equation）

对于某些线性回归问题，使用正规方程来求解参数 θ 的最优值更好。

对于目前我们使用的梯度下降方法，J(θ) 需要经过多次的迭代才能收敛到最小值。

而正规方程方法提供了一种求 θ 的解析解法，即直接进行求解，一步得到最优值。

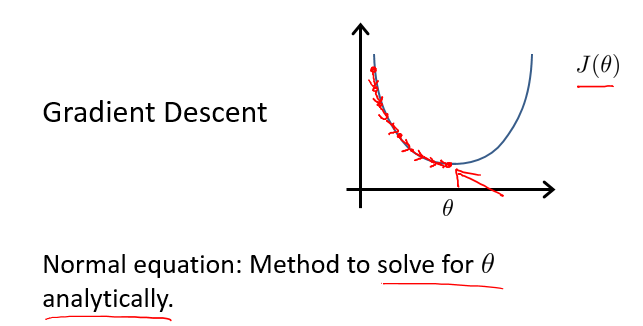
正规方程法的关键点就是对 J(θ) 进行求导，导数等于0的点极为最低点，以此求得最优的 θ ，如下图所示：

利用矩阵计算，可以方便地表示 θ 的计算过程，

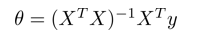
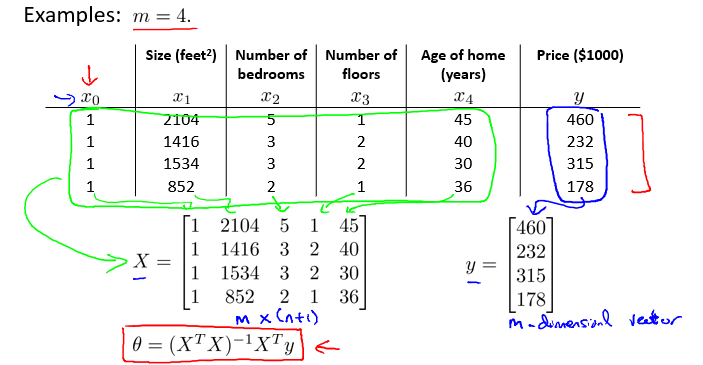
利用 matlab，可以快速地计算 θ 的最优解：

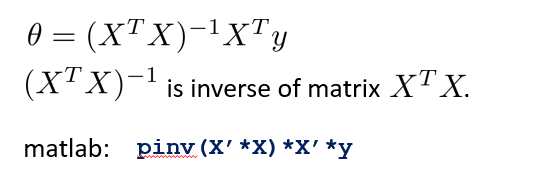
对比梯度下降和正规方程，可以发现其各有优缺点。

梯度下降需要手动的选择学习率 α ，且需要多次迭代才能得到最优解。而正规方程不需要选择学习率，也不需要迭代，可以直接求解。但是， θ 的矩阵表示虽然简单，其内部计算是相当复杂的。当特征数 n 相对较小时，使用正规方程求解相对方便。但是，当 n 很大时，正规方程将花费大量的时间进行矩阵求逆运算，这个时候，选用梯度下降方法更好。