Pytorch整理:60分钟入门
由于种种原因,近段时间开始尝试使用PyTorch。照着官方给的教程慢慢搞,稍微有一点点理解。在这里做一点小小的记录和翻译工作。

官方地址:Deep Learning with PyTorch: A 60 Minute Blitz
感谢作者:Soumith Chintala
转载请说明出处:PyTorch 整理:60 分钟入门
这个教程的目标:
- 更高层次地理解 PyTorch 的 Tensor 库以及神经网络。
- 训练一个小的神经网络模型用于分类图像。
什么是 PyTorch
这是一个基于 Python 的科学计算包,主要针对两类人群:
- 替代 Numpy 以发挥 GPU 的强大能力
- 一个提供最大灵活性和速度的深度学习研究平台
开始
Tensors
Tensors 类似于 numpy 的 ndarray,但是带了一些附加的功能,例如可以使用 GPU 加速计算等等。
构建一个未初始化的 5x3 矩阵:
import torch
x = torch.Tensor(5, 3)
print(x)
1.00000e-28 *
0.0000 0.2524 0.0000
0.2524 2.8715 0.0000
2.9158 0.0000 2.9157
0.0000 2.9158 0.0000
0.0003 0.0000 0.0000
[torch.FloatTensor of size 5x3]
构建一个随机初始化的矩阵:
x = torch.rand(5, 3)
print(x)
0.5453 0.4855 0.7236
0.3199 0.4525 0.4917
0.6965 0.8742 0.9948
0.9029 0.1873 0.0018
0.3080 0.2953 0.4313
[torch.FloatTensor of size 5x3]
获取矩阵维度大小:
print(x.size())
torch.Size([5, 3])
注意:
torch.Size实际上是一个元组,因此它支持相同的操作。
运算操作
运算操作有多种语法,让我们看看加法的例子。
加法:语法 1
y = torch.rand(5, 3)
print(x + y)
1.1177 0.8514 1.1459
1.1878 0.9249 0.5759
1.3508 1.4628 1.2833
1.8678 0.8499 0.2941
0.9718 1.0785 0.6914
[torch.FloatTensor of size 5x3]
加法:语法 2
print(torch.add(x, y))
1.1177 0.8514 1.1459
1.1878 0.9249 0.5759
1.3508 1.4628 1.2833
1.8678 0.8499 0.2941
0.9718 1.0785 0.6914
[torch.FloatTensor of size 5x3]
加法:给定一个输出 tensor
result = torch.Tensor(5, 3)
torch.add(x, y, out=result)
print(result)
1.1177 0.8514 1.1459
1.1878 0.9249 0.5759
1.3508 1.4628 1.2833
1.8678 0.8499 0.2941
0.9718 1.0785 0.6914
[torch.FloatTensor of size 5x3]
加法:就地 (in-place)
# adds x to y
y.add_(x)
print(y)
1.1177 0.8514 1.1459
1.1878 0.9249 0.5759
1.3508 1.4628 1.2833
1.8678 0.8499 0.2941
0.9718 1.0785 0.6914
[torch.FloatTensor of size 5x3]
注意:任何就地改变一个 tensor 的操作都以
_为后缀。例如:x.copy_(y),x.t_(),都会改变x。
你可以像 numpy 一样使用索引!
print(x[:, 1])
0.4855
0.4525
0.8742
0.1873
0.2953
[torch.FloatTensor of size 5]
延伸阅读:
100 + Tensor 运算,包括转置、索引、切分、数学运算、线性代数随机数等等,链接:戳这
Numpy 的桥梁
Torch 的 Tensor 和 Numpy 的数组之间的互转简直像一阵清风一样。
Torc h的 Tensor 和 Numpy 的数组会共享它们的底层存储位置,该变其中一个,另外一个也会改变。
将 Torch Tensor 转换为 Numpy 数组
a = torch.ones(5)
print(a)
1
1
1
1
1
[torch.FloatTensor of size 5]
b = a.numpy()
print(b)
[ 1. 1. 1. 1. 1.]
看看当改变 numpy 数组的值时发生了什么。
a.add_(1)
print(a)
print(b)
2
2
2
2
2
[torch.FloatTensor of size 5]
[ 2. 2. 2. 2. 2.]
将 Numpy 数组转换为 Torch Tensor
看看更改 Numpy 数组的同时自动地更改了 Torch Tensor
import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)
[ 2. 2. 2. 2. 2.]
2
2
2
2
2
[torch.DoubleTensor of size 5]
除了 CharTensor 之外,CPU 上的所有 Tensor 都支持与 Numpy 数组的来回转换。
CUDA Tensors
可以使用 .cuda 函数将 Tensor 转移到 GPU 上。
# let us run this cell only if CUDA is available
if torch.cuda.is_available():
x = x.cuda()
y = y.cuda()
x + y
Autograd: 自动求导
PyTorch 中所有神经网络的中心部分是 autograd 包。我们首先浏览一下它,然后再构建我们的第一个神经网络。
autograd 包为 Tensor 上的所有运算提供了自动求导功能。它是一个由运行定义的框架,即你的反向传播是由你的代码如何运行来决定的,而且每一轮迭代都可能是不同的。
让我们用几个简单的例子来了解几个简单的术语。
Variable 变量
autograd.Variable 是这个包的中心类。它包装一个 Tensor,并且支持几乎所有定义在这个 Tensor 上的运算。一旦你完成了你的计算,你可以调用 .backward() 来自动地计算全部的梯度。
你可以通过 .data 属性来访问最原始的 tensor,而梯度则相应地被累计到了 .grad 中。
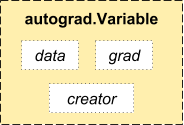
autograd 的实现中还有一个非常重要的类 - Function。
Variable 和 Function 是相互关联的并且构建了一个非循环图,其中编码了整个的计算历史。每一个变量都有一个 .creator 属性,它引用一个常见 Variable 的 Function(除了用户创建的 Variables - 它们的 creator 是 None )。
如果你想计算导数,可以在 Variable 上调用 .backward()。如果 Variable 是个标量(一个单元素数据),那么你不用为 backward() 指定任何参数,然而如果它有多个元素,你需要指定一个 grad_output 参数,它是一个匹配尺寸的 tensor。
import torch
from torch.autograd import Variable
创建一个变量:
x = Variable(torch.ones(2, 2), requires_grad=True)
print(x)
Variable containing:
1 1
1 1
[torch.FloatTensor of size 2x2]
对变量进行运算:
y = x + 2
print(y)
Variable containing:
3 3
3 3
[torch.FloatTensor of size 2x2]
y 是作为一个运算操作的结果而创建的,因而它有一个 creator
print(y.creator)
<torch.autograd._functions.basic_ops.AddConstant object at 0x108ada4a8>
在 y 上做更多的运算:
z = y * y * 3
out = z.mean()
print(z, out)
Variable containing:
27 27
27 27
[torch.FloatTensor of size 2x2]
Variable containing:
27
[torch.FloatTensor of size 1]
Gradients 梯度
让我们使用反向传播 out.backward(),它等同于 out.backward(torch.Tensor([1.0]))。
out.backward()
打印梯度 d(out)/dx:
print(x.grad)
Variable containing:
4.5000 4.5000
4.5000 4.5000
[torch.FloatTensor of size 2x2]
你应该会得到一个 4.5 的矩阵。让我们称 out 变量为 o。我们有
$$o = \frac{1}{4}\sum_i z_i$$
$$z_i = 3(x_i+2)^2$$
$$ z*i\bigr\rvert*{x_i=1} = 27 $$
因此,
$$\frac{\partial o}{\partial x_i} = \frac{3}{2}(x_i+2)$$
$$\frac{\partial o}{\partial x*i}\bigr\rvert*{x_i=1} = \frac{9}{2} = 4.5$$
你还可以使用 autograd 做一些疯狂的事情!
x = torch.randn(3)
x = Variable(x, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y = y * 2
print(y)
Variable containing:
596.2775
-807.4459
-550.6819
[torch.FloatTensor of size 3]
gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)
print(x.grad)
Variable containing:
102.4000
1024.0000
0.1024
[torch.FloatTensor of size 3]
延伸阅读:
Variable 和 Function 的文档:http://pytorch.org/docs/autograd
神经网络
神经网络可以使用 torch.nn 包来构建。
现在你大致了解了 autograd,nn 依赖于 autograd 来定义模型并进行求导。一个 nn.Module 包含多个神经网络层,以及一个 forward(input) 方法来返回 output。
例如,看看以下这个分类数字图像的网络:
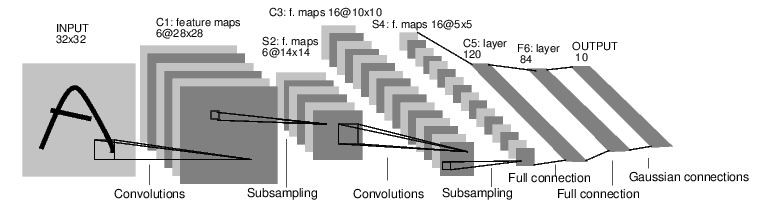
它是一个简单的前馈网络。它将输入逐步地喂给多个层,然后给出输出。
一个典型的神经网络训练过程如下:
- 定义一个拥有可学习参数(或权重)的神经网络
- 在输入数据上进行迭代
- 在网络中处理数据
- 计算损失(输出离分类正确有多远)
- 梯度反向传播给网络的参数
- 更新网络的权重,通常使用一个简单的更新规则:
weight = weight + learning_rate * gradient
定义网络
import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 图像输入通道, 6 输出通道, 5x5 正方形卷积核
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 使用 (2, 2) 窗口最大池化
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square you can only specify a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # 所有维度,除了批尺寸
num_features = 1
for s in size:
num_features *= s
return num_features
net = Net()
print(net)
Net (
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear (400 -> 120)
(fc2): Linear (120 -> 84)
(fc3): Linear (84 -> 10)
)
你只需要定义 forward 函数,backward 函数(用来计算梯度)是使用 autograd 自动为你定义的。你可以在 forward 中使用任意的 Tensor 运算操作。
模型中可学习的参数是通过 net.parameters() 返回的:
params = list(net.parameters())
print(len(params))
print(params[0].size()) # conv1's .weight
10
torch.Size([6, 1, 5, 5])
forward 的输入是一个 autograd.Variable,输出亦然。
input = Variable(torch.randn(1, 1, 32, 32))
out = net(input)
print(out)
Variable containing:
0.0455 -0.0445 0.0064 -0.0310 0.0945 -0.0362 -0.1971 0.0555 0.0943 0.1016
[torch.FloatTensor of size 1x10]
将梯度缓冲区置 0,并使用随机的梯度进行反向传播:
net.zero_grad()
out.backward(torch.randn(1, 10))
注意:
torch.nn仅支持 mini-batch。整个的torch.nn包仅支持小批量的数据,而不是一个单独的样本。例如,
nn.Conv2d应传入一个 4D 的 Tensor,维度为nSamples x nChannels x Height x Width。如果你有一个单独的样本,使用
input.unsqueeze(0)来添加一个伪批维度。
在继续之前,我们先回顾一下迄今为止的所有课程。
回顾:
torch.Tensor一个多维数组autograd.Variable包装一个 Tensor 并且记录应用在其上的历史运算操作。拥有与Tensor相同的 API,添加了一些像backward()的操作。还包括相关 tensor 的梯度。nn.Module神经网络模块。封装参数的方便方式,带有将它们转移到 GPU、导出、载入等的帮助函数。nn.Parameter一种 Variable,当给Module赋值时自动注册一个参数。autograd.Function实现一个 autograd 操作的 forward 和 backward 定义。每一个Variable操作,创建至少一个Function节点,来连接那些创建Variable的函数,并且记录其历史。
在这里,我们涵盖了:
- 定义神经网络
- 处理输入并调用 backward
还剩下:
- 计算损失
- 更新网络权重
损失函数
一个损失函数以一个 (output, target) 对为输入,然后计算一个值用以估计输出结果离目标结果多远。
存在多种的 损失函数。一个简单的损失函数:nn.MSELoss,它计算输出与目标的均方误差。
例如:
output = net(input)
target = Variable(torch.arange(1, 11)) # a dummy target, for example
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss)
Variable containing:
38.3005
[torch.FloatTensor of size 1]
现在,如果你在反方向跟随 loss,使用它的 .creator 属性,你会看到一个如下所示的计算图:
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
-> view -> linear -> relu -> linear -> relu -> linear
-> MSELoss
-> loss
因此,当我们调用 loss.backward() 时,损失对应的整个图都被求导,并且图中所有的变量都会带有累积了梯度的 .grad 属性。
print(loss.creator) # MSELoss
print(loss.creator.previous_functions[0][0]) # linear
print(loss.creator.previous_functions[0][0].previous_functions[0][0]) # ReLU
<torch.nn._functions.thnn.auto.MSELoss object at 0x10e0bdd68>
<torch.nn._functions.linear.Linear object at 0x10e0bdba8>
<torch.nn._functions.thnn.auto.Threshold object at 0x10e0bdac8>
反向传播
要进行反向传播,我们只需要调用 loss.backward()。你需要清除现有的梯度,否则梯度将累积到现有梯度。
现在我们将调用 loss.backward(),并看看 conv1 在 backward 之前和之后的梯度变化。
net.zero_grad() # zeroes the gradient buffers of all parameters
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
conv1.bias.grad before backward
Variable containing:
0
0
0
0
0
0
[torch.FloatTensor of size 6]
conv1.bias.grad after backward
Variable containing:
0.1392
-0.1155
0.0247
0.1121
-0.0559
0.0363
[torch.FloatTensor of size 6]
现在我们知道怎么使用损失函数了。
延伸阅读
神经网络包包含构建深度神经网络的多个模块和损失函数。一个完整的文档列表 在这里
仅剩的一个要学习的东西:
- 更新网络权重
更新权重
实践中最简单的更新规则是随机梯度下降(SGD):
weight = weight - learning_rate * gradient
我们可以使用简单的 Python 代码实现:
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.data * learning_rate)
然而,当您使用神经网络时,您希望使用各种不同的更新规则,例如 SGD,Nesterov-SGD,Adam,RMSProp 等等。为了实现这一点,我们构建一个小的包:torch.optim,来实现所有的方法。使用非常简单:
import torch.optim as optim
# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)
# in your training loop:
optimizer.zero_grad() # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step() # Does the update
训练一个分类器
在此,你已经知道如何定义神经网络,计算损失以及更新网络权重。
现在你可能会想,
数据怎么办
一般来说,当你处理图像、文本、音频或视频数据时,你可以使用标准的 python 包来将数据载入到 numpy 数组中。然后你可以将这个数组转化为 torch.Tensor。
- 对于图像,诸如 Pillow, OpenCV 这些包很好用。
- 对于音频,可以使用 scipy 和 librosa。
- 对于文本,要么使用原始的 Python 或 Cython 载入方式,要么使用 NLTK 和 SpaCy。
特别的对于 vision,我们创建了一个叫做 torchvision 的包,它有一些常用数据集(Imagenet, CIFAR10, MNIST 等)的数据载入器,以及图像的数据转换器, torchvision.datasets 和 torch.utils.data.DataLoader。
这提供了巨大的便利,避免编写样板代码。
在本教程中,我们使用 CIFAR10 数据集。它有 10 个类别:‘airplane’, ‘automobile’, ‘bird’, ‘cat’, ‘deer’, ‘dog’, ‘frog’, ‘horse’, ‘ship’, ‘truck’。CIFAR10 中的图像尺寸在 3x32x32,即 3 通道彩色图像,32x32 像素大小。

训练一个图像分类器
我们将按顺序完成以下步骤:
- 载入和规范化 CIFAR10 的训练和测试集,使用
torchvision - 定义一个卷积神经网络
- 定义损失函数
- 在训练集上进行训练
- 在测试集上测试网络
1. 载入和规范化 CIFAR10
使用 torchvision,载入 CIFAR10 非常简单。
import torch
import torchvision
import torchvision.transforms as transforms
torchvision datasets 的输出时范围在 [0, 1] 的 PILImage 图像。我们将它们转换为规范区间 [-1, 1] 的 Tensor。
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=True, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
让我们展示一些训练图像。
import matplotlib.pyplot as plt
import numpy as np
# functions to show image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

2. 定义一个卷积神经网络
复制在神经网络那一节的神经网络,将其更改为 3 通道图像输入(而不是原始的单通道输入)。
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
3. 定义损失函数和优化器
让我们来使用分类交叉熵和带有动量的 SGD
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
4. 训练网络
for epoch in range(10): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the input
inputs, labels = data
# wrap time in Variable
inputs, labels = Variable(inputs), Variable(labels)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.data[0]
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
[1, 2000] loss: 1.184
[1, 4000] loss: 1.206
[1, 6000] loss: 1.186
[1, 8000] loss: 1.162
[1, 10000] loss: 1.195
[1, 12000] loss: 1.165
[2, 2000] loss: 1.095
[2, 4000] loss: 1.076
[2, 6000] loss: 1.086
[2, 8000] loss: 1.092
[2, 10000] loss: 1.060
[2, 12000] loss: 1.110
[3, 2000] loss: 0.999
[3, 4000] loss: 1.005
[3, 6000] loss: 1.016
[3, 8000] loss: 1.016
[3, 10000] loss: 1.017
[3, 12000] loss: 1.023
[4, 2000] loss: 0.922
[4, 4000] loss: 0.933
[4, 6000] loss: 0.959
[4, 8000] loss: 0.975
[4, 10000] loss: 0.985
[4, 12000] loss: 0.968
[5, 2000] loss: 0.861
[5, 4000] loss: 0.908
[5, 6000] loss: 0.911
[5, 8000] loss: 0.932
[5, 10000] loss: 0.920
[5, 12000] loss: 0.919
[6, 2000] loss: 0.839
[6, 4000] loss: 0.853
[6, 6000] loss: 0.887
[6, 8000] loss: 0.891
[6, 10000] loss: 0.890
[6, 12000] loss: 0.876
[7, 2000] loss: 0.819
[7, 4000] loss: 0.808
[7, 6000] loss: 0.831
[7, 8000] loss: 0.852
[7, 10000] loss: 0.842
[7, 12000] loss: 0.869
[8, 2000] loss: 0.761
[8, 4000] loss: 0.784
[8, 6000] loss: 0.808
[8, 8000] loss: 0.827
[8, 10000] loss: 0.841
[8, 12000] loss: 0.860
[9, 2000] loss: 0.731
[9, 4000] loss: 0.758
[9, 6000] loss: 0.801
[9, 8000] loss: 0.784
[9, 10000] loss: 0.831
[9, 12000] loss: 0.817
[10, 2000] loss: 0.723
[10, 4000] loss: 0.733
[10, 6000] loss: 0.775
[10, 8000] loss: 0.763
[10, 10000] loss: 0.802
[10, 12000] loss: 0.799
Finished Training
5. 在测试数据上测试网络
我们已经在训练集上训练了 10 轮。但是我们需要检查网络是否有学到什么。
我们可以通过检测预测的类别标签,再与真实标签进行对比。如果预测是对的,我们将这个样本加到分类正确的列表中。
Okay,第一步。让我们先展示一些测试数据集中的图像。
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

再来看一下神经网络认为这些样本是什么。
输出是 10 个类别的能量。一个类别能量越高,网络就更多地认为图像是这个特定的类别。因此,让我们获取最高能量类别的索引。
outputs = net(Variable(images))
_, predicted = torch.max(outputs.data, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j][0]] for j in range(4)))
Predicted: horse plane horse frog
结果看起来不错。
让我们再来看看网络在整个数据集上的性能。
correct = 0
total = 0
for data in testloader:
images, labels = data
outputs = net(Variable(images))
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum()
print('Accuracy of the network on the 10000 test images: %d %%' % (100 * correct / total))
Accuracy of the network on the 10000 test images: 63 %
这个结果看起来远比随机抽取要好,随机抽取的概率为 10%。看起来网络确实学到了一些东西。
那么,有哪些类别表现优秀,哪些类别表现不佳呢?
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
for data in testloader:
images, labels = data
outputs = net(Variable(images))
_, predicted = torch.max(outputs.data, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i]
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s: %2d %%' % (classes[i], 100 * class_correct[i] / class_total[i]))
Accuracy of plane: 59 %
Accuracy of car: 73 %
Accuracy of bird: 51 %
Accuracy of cat: 46 %
Accuracy of deer: 51 %
Accuracy of dog: 54 %
Accuracy of frog: 76 %
Accuracy of horse: 69 %
Accuracy of ship: 78 %
Accuracy of truck: 72 %
Okay,还有什么要说明的?
如何在 GPU 上面运行这个神经网络?
在GPU上训练
与你如何将 Tensor 转移到 GPU 上类似,你可以将神经网络转移到 GPU 上。这将递归的遍历所有的模块并将它们的参数和缓存转化为 CUDA tensors。
net.cuda()
记住,你还必须在每一步将输入和结果数据传输到 GPU 上:
inputs, labels = Variable(inputs.cuda()), Variable(labels.cuda())
为什么我没有注意到相比 CPU 的巨大的加速?因为你的神经网络非常小。
训练:试着增加你的网络宽度(将第一个 nn.Conv2d 增广 2,将第二个 nn.Conv2d 增广 1 - 它们需要相同的数量),看看你的网络提速了多少。
目标达成:
- 理解 PyTorch 的 Tensor 库以及高层次的神经网络
- 训练一个小的神经网络来分类图像
转载请说明出处:PyTorch 整理:60 分钟入门
