TensorFlow (2) - 卷积神经网络
本章主要说明如何使用神经网络训练MNIST手写体字符识别,以及如何可视化权重。

这是几篇与原作不完全相同的教程。
转载请说明出处:TensorFlow (2) - 卷积神经网络
原作者:Magnus Erik Hvass Pedersen / GitHub / Videos on YouTube
在上一章节 中,我们在 MNIST 数据集上得到了 91% 的测试准确率。这个结果其实并不太理想。
在本章中,我们将使用卷积神经网络来得到一个准确率更高的模型,接近 99%。卷积神经网络使用共享的卷积核对图像进行卷积操作,以提取图像深层特征。这些深层特征然后组合成特征向量输入全连接的神经网络中,再使用类似上一章的方法进行分类。
网络结构图
在本章中需要实现的整个网络结构如下图所示:
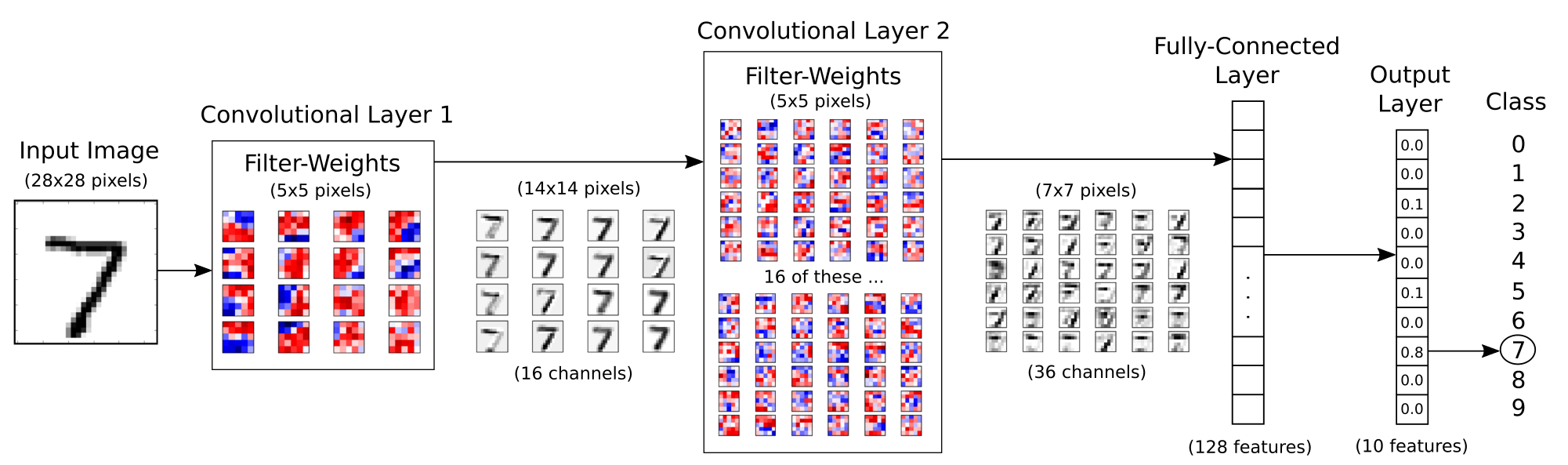
输入为原始的 28x28 的图像,它首先进入第一个拥有 16 个 5x5 卷积核的卷积层,得到 16 张 28x28 的卷积后的图像,再进入降采样层(图中未体现)最终得到 16 张 14x14 的图像(可称为 16 个通道)。为了保证卷积前后图像的像素不变,在卷积过后,对图像边框采取补零的操作(在 TensorFlow 中的 conv2d 的 padding 参数为 'SAME',如果不采取补零而是缩小像素值, padding 参数值设置为 'VALID')。降采样层使用 max pooling 操作,将 2x2 的像素块取最大值合并为一个像素点,这个操作会将图像缩小 1 倍。
对于得到的 16 通道的 14x14 图像,进入第二个拥有 36 个卷积核的卷积层,得到 36 张 14x14 的卷积后图像,再进入降采样层得到 36 张 7x7 的图像。在这里包括了一些隐含的操作,对于 16 张原始图像,每一张图像使用 36 个卷积核卷积,应该得到 16x36 张新的图像,但是为了减少模型的参数量,降低复杂度,卷积层对每个卷积核得到的 16 张图像相加,最后得到 36 张卷积后图像。
经过两层卷积后,将 36 张 7x7 的图像展平,得到一个 7x7x3 6的向量,输入到一个 128 维的全连接层,再输入到 10 维的 softmx 层进行分类,这一块与上一章类似。
卷积层
卷积层使用多个卷积核作用于同一幅图像,以得到多个卷积后的图像。如下图所示:
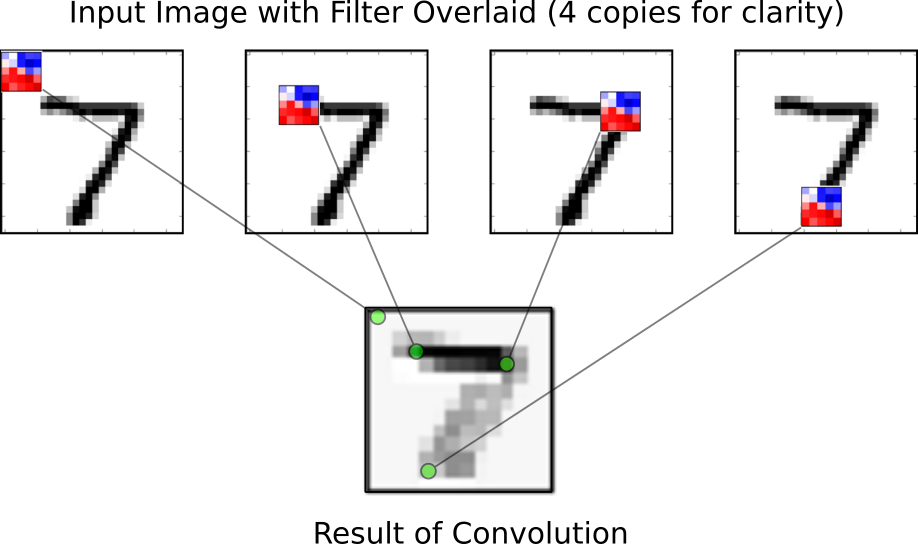
对于原始的图像 7,使用一个 5x5 的卷积核,从左到右从上到下滑动。滑动的过程称为 stride,一个卷积层有两个 stride,分别从上到下,从左到右,步长一般设定为 1 或 2。对卷积核覆盖的区域于卷积核进行点乘操作得到一个值作为该区域的中心点的像素。在上图中,红色代表这部分的像素对原始图像存在一个正的影响,而蓝色表示负的影响,在这个样例中卷积核似乎在识别图像中的横线部分,因为从结果看来 7 的那一横具有更强烈的反应。
此外,对于每一个卷积层的输出,一般会经过一个 relu 层,以保证全部的像素值都为正(因为所有为负的像素值都被设定为 0)。
需要导入的包
import tensorflow as tf # TensorFlow
import matplotlib.pyplot as plt # matplotlib绘图
import numpy as np # Numpy
from sklearn.metrics import confusion_matrix # 混淆矩阵,分析模型误差
import time # 计时
from datetime import timedelta
import math
# notebook使用
%matplotlib inline
卷积神经网络配置
# 卷积层 1
filter_size1 = 5 # 5 x 5 卷积核
num_filters1 = 16 # 共 16 个卷积核
# 卷积层 2
filter_size2 = 5 # 5 x 5 卷积核
num_filters2 = 36 # 共 36 个卷积核
# Fully-connected layer.
fc_size = 128 # Number of neurons in fully-connected layer.
载入数据
TensorFlow 在样例教程中已经做了下载并导入 MNIST 数字手写体识别数据集的实现,可以直接使用。以下代码会将 MNIST 数据集下载到 data/MNIST 目录下,将标签保存为 one-hot 编码。
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('data/MNIST', one_hot=True)
MNIST 数据集总共有 70000 张手写数字图片,数据集被分为训练集、测试集和验证集三部分。
print("数据集大小:")
print('- 训练集:{}'.format(len(data.train.labels)))
print('- 测试集:{}'.format(len(data.test.labels)))
print('- 验证集:{}'.format(len(data.validation.labels)))
数据集大小:
- 训练集:55000
- 测试集:10000
- 验证集:5000
One-hot 编码
每一张图的标签使用了 one-hot 编码保存在 numpy 矩阵中,而不是原本的类别,这是为了方便神经网络的处理。
print(data.test.labels[:5])
[[ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]]
在 one-hot 编码中,只有对应类别的那个位置为 1,其余都为 0,我们可以使用以下代码将其转换为真实类别:
data.test.cls = np.argmax(data.test.labels, axis=1)
print(data.test.cls[:5])
[7 2 1 0 4]
数据维度
在 MNIST 数据集中,原始的 28*28 像素的黑白图片被展平为 784 维的向量。
print("样本维度:", data.train.images.shape)
print("标签维度:", data.train.labels.shape)
样本维度: (55000, 784)
标签维度: (55000, 10)
为使得网络结构更加清晰,在这里对这些固定维度做如下定义:
img_size = 28 # 图片的高度和宽度
img_size_flat = img_size * img_size # 展平为向量的尺寸
img_shape = (img_size, img_size) # 图片的二维尺寸
num_channels = 1 # 输入为单通道灰度图像
num_classes = 10 # 类别数目
打印部分样例图片
def plot_images(images, cls_true, cls_pred=None):
"""
绘制图像,输出真实标签与预测标签
images: 图像(9张)
cls_true: 真实类别
cls_pred: 预测类别
"""
assert len(images) == len(cls_true) == 9 # 保证存在9张图片
fig, axes = plt.subplots(3, 3) # 创建3x3个子图的画布
fig.subplots_adjust(hspace=0.3, wspace=0.3) # 调整每张图之间的间隔
for i, ax in enumerate(axes.flat):
# 绘图,将一维向量变为二维矩阵,黑白二值图像使用 binary
ax.imshow(images[i].reshape(img_shape), cmap='binary')
if cls_pred is None: # 如果未传入预测类别
xlabel = "True: {0}".format(cls_true[i])
else:
xlabel = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i])
ax.set_xlabel(xlabel)
# 删除坐标信息
ax.set_xticks([])
ax.set_yticks([])
plt.show()
# 随机取9张图片
indices = np.arange(len(data.test.cls))
np.random.shuffle(indices)
indices = indices[:9]
images = data.test.images[indices]
cls_true = data.test.cls[indices]
plot_images(images, cls_true)
TensorFlow 计算图
TensorFlow 使用计算图模型来构建神经网络。其主要流程是先建立好整个网络的计算图模型,然后再导入数据进行计算。
一个 TensorFlow 计算图包含以下几个部分:
- Placeholder: 占位符,用来读取用户输入与输出;
- Variable: 模型的变量,也称为参数,在计算过程中逐步优化;
- Model: 使用的神经网络模型,也可以使用一些简单的计算;
- Cost Function: 代价函数,也称损失函数,如何计算模型的误差;
- Optimizer: 优化器,使用哪种优化策略来降低损失。
创建变量
def new_weights(shape):
return tf.Variable(tf.truncated_normal(shape, stddev=0.05)) # 初始化为随机值
def new_biases(length):
return tf.Variable(tf.constant(0.05, shape=[length])) # 初始化为常数
卷积神经网络中同样有两类变量,权重和偏置项。注意,这里的初始化只有在运行计算图时才会执行。
创建卷积层
这个函数创建了一个卷积层。输入为 4 维的 tensor,维度如下:
- 图像数量
- 图像高度
- 图像宽度
- 通道数
输出同样是一个 4 维的 tensor,维度如下:
- 图像数量,与输入相同
- 图像高度,如果使用 2x2 pooling,高宽都除以 2
- 图像宽度,同上
- 由卷积层生成的通道数
def new_conv_layer(input, # 前一层.
num_input_channels, # 前一层通道数
filter_size, # 卷积核尺寸
num_filters, # 卷积核数目
use_pooling=True): # 使用 2x2 max-pooling.
# 卷积核权重的形状,由TensorFlow API决定
shape = [filter_size, filter_size, num_input_channels, num_filters]
# 根据跟定形状创建权重
weights = new_weights(shape=shape)
# 创建新的偏置,每个卷积核一个偏置
biases = new_biases(length=num_filters)
# 创建卷积层。注意stride全设置为1。
# 第1个和第4个必须是1,因为第1个是图像的数目,第4个是图像的通道。
# 第2和第3指定和左右、上下的步长。
# padding设置为'SAME' 意味着给图像补零,以保证前后像素相同。
layer = tf.nn.conv2d(input=input,
filter=weights,
strides=[1, 1, 1, 1],
padding='SAME')
# 给卷积层的输出添加一个偏置,每个卷积通道一个偏置值
layer += biases
# 是否使用pooling
if use_pooling:
# 这是 2x2 max-pooling, 表明使用 2x2 的窗口,选择每一窗口的最大值作为该窗口的像素,
# 然后移动2格到下一窗口。
layer = tf.nn.max_pool(value=layer,
ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1],
padding='SAME')
# Rectified Linear Unit (ReLU).
# 对每个输入像素x,计算 max(x, 0),把负数的像素值变为0.
# 这一步为原输出添加了一定的非线性特性,允许我们学习更加复杂的函数。
layer = tf.nn.relu(layer)
# 注意 relu 通常在pooling前执行,但是由于 relu(max_pool(x)) == max_pool(relu(x)),
# 我们可以通过先max_pooling再relu省去75%的计算。
# 返回结果层和权重,结果层用于下一层输入,权重用于显式输出
return layer, weights
展平操作
一个卷积层的输出为 4 维度的 tensor。我们需要在卷积层后添加一个全连接层,首先得将 4 为的 tensor 展平为 2 维的 tensor,这样才能直接输入到全连接层。
def flatten_layer(layer):
# 获取输入层的形状,
# layer_shape == [num_images, img_height, img_width, num_channels]
layer_shape = layer.get_shape()
# 特征数量: img_height * img_width * num_channels
# 可以使用TensorFlow内建操作计算.
num_features = layer_shape[1:4].num_elements()
# 将形状重塑为 [num_images, num_features].
# 注意只设定了第二个维度的尺寸为num_filters,第一个维度为-1,保证第一个维度num_images不变
# 展平后的层的形状为:
# [num_images, img_height * img_width * num_channels]
layer_flat = tf.reshape(layer, [-1, num_features])
return layer_flat, num_features
创建全连接层
def new_fc_layer(input, # 前一层.
num_inputs, # 前一层输入维度
num_outputs, # 输出维度
use_relu=True): # 是否使用RELU
# 新的权重和偏置,与第一章一样.
weights = new_weights(shape=[num_inputs, num_outputs])
biases = new_biases(length=num_outputs)
# 计算 y = wx + b,同第一章
layer = tf.matmul(input, weights) + biases
# 是否使用RELU
if use_relu:
layer = tf.nn.relu(layer)
return layer
Placeholder 占位符
占位符为输入与输出占据位置,这些输入输出一般在不同的轮次都会有所变化。由于 TensorFlow 先构图再计算,所以需要使用占位符为输入和输出预留位置。
x = tf.placeholder(tf.float32, shape=[None, img_size_flat], name='x') # 原始输入
x_image = tf.reshape(x, [-1, img_size, img_size, num_channels]) # 转换为2维图像
y_true = tf.placeholder(tf.float32, shape=[None, num_classes], name='y_true') # 原始输出
y_true_cls = tf.argmax(y_true, axis=1) # 转换为真实类别,与之前的使用placeholder不同
卷积层 1
layer_conv1, weights_conv1 = \\
new_conv_layer(input=x_image, # 输入图像
num_input_channels=num_channels, # 输入通道数
filter_size=filter_size1, # 卷积核尺寸
num_filters=num_filters1, # 卷积核数目
use_pooling=True)
print(layer_conv1)
Tensor("Relu:0", shape=(?, 14, 14, 16), dtype=float32)
输入为 (?, 28, 28, 1) 的图像,其中 ? 为图像数量。可以看到,第一个卷积层的输入为 (?, 14, 14, 16) 的 tensor,即 14x14 像素的 16 道图像。
卷积层 2
layer_conv2, weights_conv2 = \\
new_conv_layer(input=layer_conv1,
num_input_channels=num_filters1,
filter_size=filter_size2,
num_filters=num_filters2,
use_pooling=True)
print(layer_conv2)
Tensor("Relu_1:0", shape=(?, 7, 7, 36), dtype=float32)
解释同上,输入为上一层的输出。
展平层
展平层将第二个卷积层展平为二维 tensor。
layer_flat, num_features = flatten_layer(layer_conv2)
print(layer_flat)
Tensor("Reshape_1:0", shape=(?, 1764), dtype=float32)
输出为 (?, 1764) 的 tensor。
全连接层 1
layer_fc1 = new_fc_layer(input=layer_flat, # 展平层输出
num_inputs=num_features, # 输入特征维度
num_outputs=fc_size, # 输出特征维度
use_relu=True)
print(layer_fc1)
Tensor("Relu_2:0", shape=(?, 128), dtype=float32)
输出为 (?, 128) 的 2 维 tensor。
全连接层 2
layer_fc2 = new_fc_layer(input=layer_fc1, # 上一全连接层
num_inputs=fc_size, # 输入特征维度
num_outputs=num_classes, # 输出类别数
use_relu=False)
print(layer_fc2)
Tensor("add_3:0", shape=(?, 10), dtype=float32)
输出为 (?, 10) 的二维 tensor,意在判定输入图像属于哪一类, 注意该层未使用 relu,因为将要输入到后续的 softmax 中。
预测类别
第二个全连接层估计输入的图像属于某一类别的程度,这个估计有些粗糙,需要添加一个 softmax 层归一化为概率表示。
y_pred = tf.nn.softmax(layer_fc2) # softmax归一化
y_pred_cls = tf.argmax(y_pred, axis=1) # 真实类别
代价函数
这一部分与上一章的类似。
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=layer_fc2,
labels=y_true)
cost = tf.reduce_mean(cross_entropy)
优化方法
这一部分与上一章类似,但是优化器使用改进版的梯度下降,Adam。
optimizer = tf.train.AdamOptimizer(learning_rate=1e-4).minimize(cost)
性能度量
同上一章
correct_prediction = tf.equal(y_pred_cls, y_true_cls)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
运行 TensorFlow 计算图
创建 Session 以及变量初始化
TensorFlow 计算图运行在一个 session 中,计算之前需要先创建这个 session,并初始化其中的一些变量(w 和 b),TensorFlow 使用 session.run() 来运行计算图。
session = tf.Session() # 创建session
session.run(tf.global_variables_initializer()) # 变量初始化
执行优化的帮助函数
同第一章,添加了部分状态输出的代码:
train_batch_size = 64
# 计算目前执行的总迭代次数
total_iterations = 0
def optimize(num_iterations):
# 保证更新全局变量.
global total_iterations
# 用来输出用时.
start_time = time.time()
for i in range(total_iterations, total_iterations + num_iterations):
# 获取一批数据,放入dict,同第一章
x_batch, y_true_batch = data.train.next_batch(train_batch_size)
feed_dict_train = {x: x_batch,
y_true: y_true_batch}
# 运行优化器
session.run(optimizer, feed_dict=feed_dict_train)
# 每100轮迭代输出状态
if i % 100 == 0:
# 计算训练集准确率.
acc = session.run(accuracy, feed_dict=feed_dict_train)
msg = "迭代轮次: {0:>6}, 训练准确率: {1:>6.1%}"
print(msg.format(i + 1, acc))
total_iterations += num_iterations
end_time = time.time()
time_dif = end_time - start_time
# 输出用时.
print("用时: " + str(timedelta(seconds=int(round(time_dif)))))
输出部分错误样例和混淆矩阵
与上一章类似。
def plot_example_errors(cls_pred, correct):
# 计算错误情况
incorrect = (correct == False)
images = data.test.images[incorrect]
cls_pred = cls_pred[incorrect]
cls_true = data.test.cls[incorrect]
# 随机挑选9个
indices = np.arange(len(images))
np.random.shuffle(indices)
indices = indices[:9]
plot_images(images[indices], cls_true[indices], cls_pred[indices])
def plot_confusion_matrix(cls_pred):
cls_true = data.test.cls # 真实类别
# 使用scikit-learn的confusion_matrix来计算混淆矩阵
cm = confusion_matrix(y_true=cls_true, y_pred=cls_pred)
# 打印混淆矩阵
print(cm)
# 将混淆矩阵输出为图像
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
# 调整图像
plt.tight_layout()
plt.colorbar()
tick_marks = np.arange(num_classes)
plt.xticks(tick_marks, range(num_classes))
plt.yticks(tick_marks, range(num_classes))
plt.xlabel('Predicted')
plt.ylabel('True')
plt.show()
显示性能的帮助函数
用来输出测试准确率的的函数。计算所有图像的分类需要一定的时间,因此我们在上面定义的一些函数中重用了分类结果。这个函数会占据大量的内存,所以将测试集分成了多个小的批次。如果你的机器内存太小,你可以尝试减小 batch_size。
# 将测试集分成更小的批次
test_batch_size = 256
def print_test_accuracy(show_example_errors=False,
show_confusion_matrix=False):
# 测试集图像数量.
num_test = len(data.test.images)
# 为预测结果申请一个数组.
cls_pred = np.zeros(shape=num_test, dtype=np.int)
# 数据集的起始id为0
i = 0
while i < num_test:
# j为下一批次的截止id
j = min(i + test_batch_size, num_test)
# 获取i,j之间的图像
images = data.test.images[i:j, :]
# 获取相应标签.
labels = data.test.labels[i:j, :]
# 创建feed_dict
feed_dict = {x: images,
y_true: labels}
# 计算预测结果
cls_pred[i:j] = session.run(y_pred_cls, feed_dict=feed_dict)
# 设定为下一批次起始值.
i = j
cls_true = data.test.cls
# 正确的分类
correct = (cls_true == cls_pred)
# 正确分类的数量
correct_sum = correct.sum()
# 分类准确率
acc = float(correct_sum) / num_test
# 打印准确率.
msg = "测试集准确率: {0:.1%} ({1} / {2})"
print(msg.format(acc, correct_sum, num_test))
# 打印部分错误样例.
if show_example_errors:
print("Example errors:")
plot_example_errors(cls_pred=cls_pred, correct=correct)
# 打印混淆矩阵.
if show_confusion_matrix:
print("Confusion Matrix:")
plot_confusion_matrix(cls_pred=cls_pred)
优化前的性能测试
print_test_accuracy()
测试集准确率: 4.2% (424 / 10000)
可以看到,测试的准确率极低,但是函数的功能正常。
执行一轮优化后的性能
optimize(num_iterations=1)
print_test_accuracy()
迭代轮次: 1, 训练准确率: 3.1%
用时: 0:00:00
测试集准确率: 5.3% (534 / 10000)
一轮迭代后,性能稍有提升。
100 轮优化后的性能
optimize(num_iterations=99)
print_test_accuracy()
用时: 0:00:08
测试集准确率: 70.8% (7077 / 10000)
可以看到,执行 100 轮迭代后,性能存在大幅度提升。
1000 轮优化后性能
optimize(num_iterations=900)
print_test_accuracy(show_example_errors=True)
迭代轮次: 101, 训练准确率: 70.3%
迭代轮次: 201, 训练准确率: 87.5%
迭代轮次: 301, 训练准确率: 84.4%
迭代轮次: 401, 训练准确率: 84.4%
迭代轮次: 501, 训练准确率: 95.3%
迭代轮次: 601, 训练准确率: 90.6%
迭代轮次: 701, 训练准确率: 95.3%
迭代轮次: 801, 训练准确率: 89.1%
迭代轮次: 901, 训练准确率: 93.8%
用时: 0:01:12
测试集准确率: 93.5% (9351 / 10000)
Example errors:

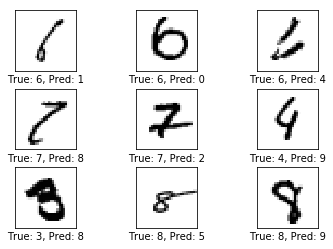
可以发现,测试集的准确率为 93.5%,已经比第一章的 91.9% 要高。输出的部分错误样例显示,部分形状相似的数字仍然难以区分。
10000 轮次优化后的性能
optimize(num_iterations=9000)
print_test_accuracy(show_example_errors=True,
show_confusion_matrix=True)
迭代轮次: 1001, 训练准确率: 93.8%
迭代轮次: 1101, 训练准确率: 92.2%
迭代轮次: 1201, 训练准确率: 95.3%
迭代轮次: 1301, 训练准确率: 98.4%
迭代轮次: 1401, 训练准确率: 96.9%
迭代轮次: 1501, 训练准确率: 92.2%
迭代轮次: 1601, 训练准确率: 96.9%
迭代轮次: 1701, 训练准确率: 92.2%
迭代轮次: 1801, 训练准确率: 98.4%
迭代轮次: 1901, 训练准确率: 98.4%
迭代轮次: 2001, 训练准确率: 98.4%
迭代轮次: 2101, 训练准确率: 93.8%
迭代轮次: 2201, 训练准确率: 98.4%
迭代轮次: 2301, 训练准确率: 93.8%
迭代轮次: 2401, 训练准确率: 96.9%
迭代轮次: 2501, 训练准确率: 95.3%
迭代轮次: 2601, 训练准确率: 95.3%
迭代轮次: 2701, 训练准确率: 95.3%
迭代轮次: 2801, 训练准确率: 100.0%
迭代轮次: 2901, 训练准确率: 96.9%
迭代轮次: 3001, 训练准确率: 90.6%
迭代轮次: 3101, 训练准确率: 98.4%
迭代轮次: 3201, 训练准确率: 98.4%
迭代轮次: 3301, 训练准确率: 98.4%
迭代轮次: 3401, 训练准确率: 96.9%
迭代轮次: 3501, 训练准确率: 96.9%
迭代轮次: 3601, 训练准确率: 96.9%
迭代轮次: 3701, 训练准确率: 100.0%
迭代轮次: 3801, 训练准确率: 96.9%
迭代轮次: 3901, 训练准确率: 98.4%
迭代轮次: 4001, 训练准确率: 96.9%
迭代轮次: 4101, 训练准确率: 96.9%
迭代轮次: 4201, 训练准确率: 98.4%
迭代轮次: 4301, 训练准确率: 98.4%
迭代轮次: 4401, 训练准确率: 98.4%
迭代轮次: 4501, 训练准确率: 96.9%
迭代轮次: 4601, 训练准确率: 100.0%
迭代轮次: 4701, 训练准确率: 96.9%
迭代轮次: 4801, 训练准确率: 98.4%
迭代轮次: 4901, 训练准确率: 98.4%
迭代轮次: 5001, 训练准确率: 93.8%
迭代轮次: 5101, 训练准确率: 98.4%
迭代轮次: 5201, 训练准确率: 92.2%
迭代轮次: 5301, 训练准确率: 96.9%
迭代轮次: 5401, 训练准确率: 98.4%
迭代轮次: 5501, 训练准确率: 98.4%
迭代轮次: 5601, 训练准确率: 98.4%
迭代轮次: 5701, 训练准确率: 98.4%
迭代轮次: 5801, 训练准确率: 95.3%
迭代轮次: 5901, 训练准确率: 96.9%
迭代轮次: 6001, 训练准确率: 100.0%
迭代轮次: 6101, 训练准确率: 98.4%
迭代轮次: 6201, 训练准确率: 100.0%
迭代轮次: 6301, 训练准确率: 100.0%
迭代轮次: 6401, 训练准确率: 100.0%
迭代轮次: 6501, 训练准确率: 98.4%
迭代轮次: 6601, 训练准确率: 100.0%
迭代轮次: 6701, 训练准确率: 95.3%
迭代轮次: 6801, 训练准确率: 100.0%
迭代轮次: 6901, 训练准确率: 100.0%
迭代轮次: 7001, 训练准确率: 100.0%
迭代轮次: 7101, 训练准确率: 98.4%
迭代轮次: 7201, 训练准确率: 100.0%
迭代轮次: 7301, 训练准确率: 96.9%
迭代轮次: 7401, 训练准确率: 100.0%
迭代轮次: 7501, 训练准确率: 100.0%
迭代轮次: 7601, 训练准确率: 98.4%
迭代轮次: 7701, 训练准确率: 98.4%
迭代轮次: 7801, 训练准确率: 100.0%
迭代轮次: 7901, 训练准确率: 100.0%
迭代轮次: 8001, 训练准确率: 95.3%
迭代轮次: 8101, 训练准确率: 98.4%
迭代轮次: 8201, 训练准确率: 96.9%
迭代轮次: 8301, 训练准确率: 98.4%
迭代轮次: 8401, 训练准确率: 98.4%
迭代轮次: 8501, 训练准确率: 100.0%
迭代轮次: 8601, 训练准确率: 96.9%
迭代轮次: 8701, 训练准确率: 98.4%
迭代轮次: 8801, 训练准确率: 98.4%
迭代轮次: 8901, 训练准确率: 96.9%
迭代轮次: 9001, 训练准确率: 100.0%
迭代轮次: 9101, 训练准确率: 100.0%
迭代轮次: 9201, 训练准确率: 98.4%
迭代轮次: 9301, 训练准确率: 100.0%
迭代轮次: 9401, 训练准确率: 98.4%
迭代轮次: 9501, 训练准确率: 98.4%
迭代轮次: 9601, 训练准确率: 100.0%
迭代轮次: 9701, 训练准确率: 100.0%
迭代轮次: 9801, 训练准确率: 98.4%
迭代轮次: 9901, 训练准确率: 100.0%
用时: 0:12:42
测试集准确率: 98.7% (9873 / 10000)
Example errors:
Confusion Matrix:
[[ 974 0 1 0 0 1 1 1 2 0]
[ 0 1130 1 0 0 1 0 2 1 0]
[ 4 1 1020 0 1 0 0 3 3 0]
[ 1 0 1 1000 0 3 0 2 3 0]
[ 0 0 2 0 968 0 1 2 2 7]
[ 2 0 0 6 0 878 2 2 1 1]
[ 5 2 0 0 2 2 945 0 2 0]
[ 1 0 7 2 0 0 0 1016 1 1]
[ 5 0 2 1 0 2 0 2 959 3]
[ 2 5 1 3 4 4 0 5 2 983]]

经过 10000 轮迭代后,测试集的准确率达到了 98.7% 的准确率。在分错的样本中,部分用肉眼也难以分辨。而混淆矩阵表明绝大部分的样本都分类正确。这是一个非常好的模型。
权重和层的可视化
为了更好的理解卷积神经网络为何能识别手写体数字,我来来可视化部分权重和层输出。
卷积权重可视化
def plot_conv_weights(weights, input_channel=0):
# weights_conv1 or weights_conv2.
# 运行weights以获得权重
w = session.run(weights)
# 获取权重最小值最大值,这将用户纠正整个图像的颜色密集度,来进行对比
w_min = np.min(w)
w_max = np.max(w)
# 卷积核树木
num_filters = w.shape[3]
# 需要输出的卷积核
num_grids = math.ceil(math.sqrt(num_filters))
fig, axes = plt.subplots(num_grids, num_grids)
for i, ax in enumerate(axes.flat):
# 只输出有用的子图.
if i<num_filters:
# 获得第i个卷积核在特定输入通道上的权重
img = w[:, :, input_channel, i]
ax.imshow(img, vmin=w_min, vmax=w_max,
interpolation='nearest', cmap='seismic')
# 移除坐标.
ax.set_xticks([])
ax.set_yticks([])
plt.show()
卷积层输出可视化
def plot_conv_layer(layer, image):
# layer_conv1 or layer_conv2.
# feed_dict只需要x,标签信息在此不需要.
feed_dict = {x: [image]}
# 获取该层的输出结果
values = session.run(layer, feed_dict=feed_dict)
# 卷积核树木
num_filters = values.shape[3]
# 每行需要输出的卷积核网格数
num_grids = math.ceil(math.sqrt(num_filters))
fig, axes = plt.subplots(num_grids, num_grids)
for i, ax in enumerate(axes.flat):
# 只输出有用的子图.
if i<num_filters:
# 获取第i个卷积核的输出
img = values[0, :, :, i]
ax.imshow(img, interpolation='nearest', cmap='binary')
# 移除坐标.
ax.set_xticks([])
ax.set_yticks([])
plt.show()
打印输入图像
def plot_image(image):
plt.imshow(image.reshape(img_shape),
interpolation='nearest',
cmap='binary')
plt.show()
打印第一章图像:
image1 = data.test.images[0]
plot_image(image1)

打印另一张图像:
image2 = data.test.images[13]
plot_image(image2)

卷积层 1
plot_conv_weights(weights=weights_conv1)
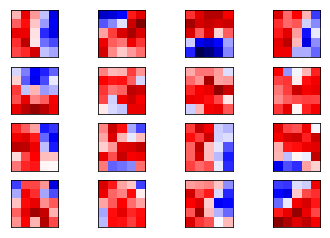
以上就是 16 个卷积核在第一个通道的权重情况。其中红色为正的权重,蓝色为负的权重。在这里我们很难判别这些权重是如何起作用的。
将 image1 喂入卷积层 1,得到使用不同卷积后得到的图像,这些图像的棱角更加分明,而且在不同的边的突出情况也不同:
plot_conv_layer(layer=layer_conv1, image=image1)

将 image2 喂入卷积层 1,得到如下图像,在不同部位的突出情况不同:
plot_conv_layer(layer=layer_conv1, image=image2)

卷积层 2
现在输出第二个卷积层的权重。
由于卷积层 1 有 16 个输出通道,这意味着卷积层 2 有 16 个输入通道,每个通道的输入又对应 36 个输出通道,因此总共有 16x36 个通道的卷积核。我们先输出第一个通道的卷积核。
plot_conv_weights(weights=weights_conv2, input_channel=0)
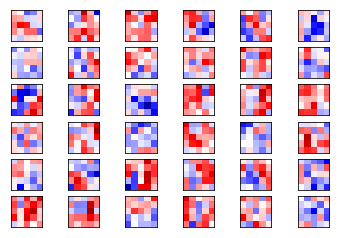
这些权重相对与卷积层1的权重更加抽象,无法用语言来解释。接下来输出第二个通道的卷积核。
plot_conv_weights(weights=weights_conv2, input_channel=1)
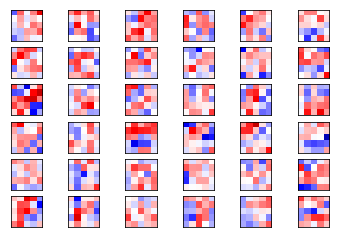
可以说明,不同输入通道对应的卷积核是不同的。将image1在卷积层1的输出再次输入卷积层2,得到如下输出:
plot_conv_layer(layer=layer_conv1, image=image2)

image2的输出如下:
plot_conv_layer(layer=layer_conv1, image=image2)

所输出的图像达到了一个更高的层次,卷积核试图提取一些边缘化的特征,这些特征对于同类图像的变化并不敏感。
在运行完整个计算图后,需要将它关闭,否则将一直占用资源:
session.close()
